
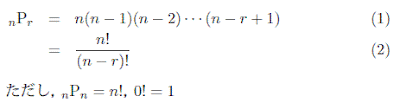
That is, to each of those 4 ways there correspond 3. After that has happened, there are 3 ways to choose the second. We can draw the first in 4 different ways: either a or b or c or d. If something can be chosen, or can happen, or be done, in m different ways, and, after that has happened, something else can be chosen in n different ways, then the number of ways of choosing both of them is m įor example, imagine putting the letters a, b, c, d into a hat, and then drawing two of them in succession. It is derived theoretically from the Fundamental Principle of Counting: Now, this enormous number was not found by counting them. For example, if twelve different things are permuted, then the number of their permutations is 479,001,600. As the number of things (letters) increases, their permutations grow astronomically. There are 6 permutations of three different things. Try the given examples, or type in your own problem and check your answer with the step-by-step explanations.ī Y THE PERMUTATIONS of the letters abc we mean all of their possible arrangements:
#19 permute 3 free
Try the free Mathway calculator and problem solver below to practice various math topics.
We can use the permutation formula P(6, 6) which is 6 things taken 6 at a time. In how many ways can 6 people be seated in a row of 6 chairs? In this example, the symbol P(3, 3) represents the number of permutations of 3 things taken 3 at a time. There are 3 choices for the first boy, 2 choices for the second and 1 choice for the third, so the total number of permutations is 3 x 2 x 1 = 6. They can be arranged in any of several ways. In how many ways can the boys be arranged? Suppose we want to take a picture of three boys, Allen, Bryan and Carlos. In another lesson, we will consider the number of permutations of n things taken r at a time. In this lesson, we will look at examples of the number of permutations of n things taken n at a time. So out of that set of 4 horses you want to pick the subset of 3 winners and the order in which they finish.Ī permutation is an arrangement, or listing, of objects in which the order is important. In a race of 15 horses you beleive that you know the best 4 horses and that 3 of them will finish in the top spots: win, place and show (1st, 2nd and 3rd). Now v5 contains the horizontal max in all of its components. Permute v3 to v4, swapping the 0th and 1st elements, and the 2nd and 3rd ones.


 0 kommentar(er)
0 kommentar(er)
